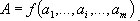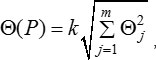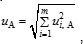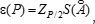Испытательная лаборатория. К вопросу оценки погрешностей измерений

Автор: Кондратьев А.В.

Ну вот, рассмотрев и обсудив в весьма значительном количестве публикаций самые разнообразные измерения физических величин, пойдём дальше. А дальше у нас обработка результатов, то есть расчёты. Разумеется, собственно расчётов, то есть вычисления значений параметров защищённости для различных ТКУИ мы здесь рассматривать не будем. Не время и не место J

Но есть одна проблема, которую озвучивают уже много лет, но её практическое воплощение не приблизилось ни на йоту L Это вопросы оценки (и расчёта) погрешностей выполненных измерений. Вот о ней и поговорим (в очередной раз), однако постараюсь быть конкретным.

Итак, пользуясь установленной терминологией, можно утверждать, что подавляющее число наших измерений есть измерения прямые. Это однозначно по отношению к, например, измерениям в области АВАК (акустика и вибрации) – измеряются звуковое давление и/или виброускорение; измерениям в области НЧ АЭП – измеряется напряжение переменного тока; частично ВЧ АЭП - измеряются индекс или коэффициент модуляции (если измерение выполняется системой «Талис»); частично ПЭМИН – при измерениях наводок измеряется напряжение или сила тока в линии.

Измерения напряжённости полей (как ВЧ - в СИ ПЭМИ или ВЧ АЭП или НЧ – в СИ АЭП (по НЧ полям)), в общем случае, приходится отнести к косвенным методам измерения. Не будем голословными:

В соответствии с МИ 2083-90 ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей.

Цитата:

1. ОБЩИЕ ПОЛОЖЕНИЯ 1.1. Искомое значение физической величины А находят на основании результатов измерений аргументов а1, . . . , а i , . . . , а m , связанных с искомой величиной уравнением ( 1 ) Функция f должна быть известна из теоретических предпосылок или установлена экспериментально с погрешностью, которой можно пренебречь.

Именно так и выполняются любые измерения напряжённости поля (или неконтактные измерения силы тока при помощи токоизмерителя). Поскольку непосредственно измеряемая величина – это напряжение переменного тока на выходе первичного преобразователя в В (в абсолютных единицах или в дБ). А напряжённостью поля она становится только после прибавления (если в дБ) «антенного коэффициента». Именно в соответствии с уравнением:

Где:

U_изм - показания измерительного приёмника (анализатора), дБ;

K_а - коэффициент, калибровки преобразователя на частоте измерения, дБ

Данная зависимость выведена из теоретических предпосылок и его погрешность пренебрежимо мала (чего никак нельзя сказать о погрешности аргументов, в него входящих).

При линейной зависимости в основном уравнении предписывается суммарную погрешность рассчитывать (в соответствии с уже процитированными Методическими указаниями) так:

Искомое значение A связано с m измеряемыми аргументами a₁, a² , . . . , a_m уравнением

A = b₁a₁ + b₂ · a₂, + ...+ b_m · a_m ,

(2)

где:

b₁, b₂,...b_m - постоянные коэффициенты при аргументах a₁, a₂ . . . , a_m соответственно.

Корреляция между погрешностями измерений аргументов отсутствует.

Результат косвенного измерения  вычисляют по формуле:

где:

a_i - результат измерения аргумента;

m - число аргументов.

Предписания в отношении определения доверительных границ случайной погрешности результата косвенного измерения опустим (пока) до того момента, когда будет официализована хоть какая-то разумная методика оценки погрешности J

Отметим только что вычисляется среднеквадратическое отклонение результата, находятся границы неисключённой систематической погрешности, и, наконец, погрешность результата косвенного измерения оценивают (вычисляют) на основе композиции распределений случайных и неисключенных систематических погрешностей :)

Вообще-то стоило бы привести весь документ, в целом. Изложено всё вполне воспринимаемым языком и логично.

Однако, при внимательном рассмотрении, сознание немедленно отмечает – «что-то не вяжется!». И действительно…

Предложенный механизм расчёта погрешности базируется на том, что ОДНО И ТОЖЕ значение измеряется НЕСКОЛЬКО раз. Тогда всё понятно и логично. Есть из чего вычислять отклонение и всё последующее.

Но у нас-то, в огромном большинстве случаев, измерения ОДНОКРАТНЫЕ!!!! Особенно сегодня, любой Заказчик придёт в тихий (а скорее – в агрессивный) ступор, если ему сообщить, что надо выполнить не «один», а, например, пятикратный объём измерений (естественно, им, Заказчиком, оплаченный) чтобы «вычислить погрешность»… Со 100% вероятностью нас «пошлют» всерьёз и далеко…

Посмотрим, что наработала метрология для такого варианта.

Изучаем систему метрологических НМД и … обнаруживаем: Р 50.2.038-2004 Государственная система обеспечения единства измерений. Измерения прямые однократные. Оценивание погрешностей и неопределенности результата измерений.

Это уже заметно ближе. Хотя и относится только к прямым измерениям. Однако рассмотрим, а потом порассуждаем, нельзя ли каким-то боком это распространить и на измерения косвенные.

Наиболее интереснен для анализа, вначале, 5 раздел. Позволю себе процитировать его полностью:

5 Составляющие погрешности и неопределенности результата измерения 5.1 Составляющими погрешности результата однократного измерения являются погрешности СИ (СИ — средство измерений), метода, оператора, а также погрешности, обусловленные изменением условий измерения. 5.2 Погрешность результата однократного измерения чаще всего представлена НСП (НСП — неисключенная систематическая погрешность) и случайными погрешностями. Неопределенность результата однократного измерения может быть представлена стандартными неопределенностями, оцениваемыми по типам А и В. 5.3 Характеристикой НСП могут быть: - границы ± Θ; - доверительные границы ± Θ(Р). 5.4 Характеристикой случайных погрешностей могут быть: - СКО S; - доверительные границы ± e(Р). 5.5 Погрешность СИ определяют на основании их метрологических характеристик, которые должны быть указаны в нормативных и технических документах, и в соответствии с РД 50-453. 5.6 Погрешности метода и оператора должны быть определены при разработке и аттестации конкретной МВИ.

Из этого перечисления нам, реально, доступны:

- Погрешность СИ (приведена в Свидетельстве о поверке);

- В какой-то мере – погрешности оператора

В общем-то всё… Об остальном можно только рассуждать, причём, чаще всего, без должной доказательной базы. Хотя уже десятилетия называются цифры «погрешности» измерений напряжённости поля в ближней зоне от 30 до 150%, погрешность от произвольной установки (выборе места размещения или подключения) пробника или токоизмерителя на линии от 50 до 1000% и т.д. Однако реальных, с достаточно надёжной статистикой, «официальных» результатов нет.

Насколько известно автору, в «ранешнее» время, при зарождении проблематики, пошли самым простым путём. Во многие методики, нормы и т.д. просто были заложены «запасы» на любые возможные погрешности. Эдак процентов на 200÷500%...

Надо бы всё это пересмотреть, пересчитать и … Всё верно, но вопрос плавно перетёк в абсолютно другую плоскость – кто за проведение этой (весьма объёмной и не очень простой) работы заплатит? Не будем мучатся риторическими вопросами, толку-то…

Если «забыть» о погрешности метода и, в какой-то степени, о погрешности, обусловленные изменением условий измерения, то останется именно то, что оценить возможно.

С погрешностью СИ (приёмника, анализатора, вольтметра…) проще всего, тривиально. Но если попытаться «распространить» положения рассматриваемого РД на измерения косвенные, то, по сути, эта сама погрешность СИ оказывается линейной функцией (вспомним рассуждения в соответствии с МИ 2083-90 ГСИ) трёх аргументов:

– погрешности именно средства измерения, погрешностью поверки (калибровки. Вообще-то понятие калибровки исключено 102 ФЗ, но… живучая она!);

– первичного преобразователя (антенны, токоизмерителя, пробника…);

– и, самое неопределённое, погрешностью нахождения значения Ка по табличным (методом интерполяции) или графическим представлениям.

Впрочем, определить границы этой, последней, погрешности, относительно несложно. Проанализировать применяемые для этого случая методы интерполяции, задать однозначно применение одного конкретного (единого для всех), запретить всяческие «ручные» методы (при сегодняшнем развитии средств ЭВТ иное просто смешно!). И границы определяться сами собой.

Дальше всё несложно, в точном соответствии с РД:

Цитата:

6.1 НСП результата измерения выражают границами этой погрешности, если среди составляющих погрешности результата измерения в наличии одна НСП. При указанном выше условии стандартную неопределенность uВ, обусловленную неисключенной систематической погрешностью, заданной своими границами ± Q, оценивают по формуле (2). 6.2 Доверительные границы НСП результата измерения вычисляют следующим образом. 6.2.1 При наличии нескольких НСП, заданных своими границами ± Θj, доверительную границу НСП результата измерения Θ(Р) (без учета знака) вычисляют по формуле  (5) где k — поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих Θj. При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1. При доверительной вероятности Р = 0,99 поправочный коэффициент k принимают равным 1,45, если число суммируемых составляющих m > 4. Если же число составляющих равно четырем (m = 4), то поправочный коэффициент k ≈ 1,4; при m = 3 k ≈ 1,3; при m = 2 k ≈ 1,2. Более точное значение k для доверительной вероятности Р = 0,99 при числе составляющих m £ 4 в зависимости от соотношения составляющих I определяют по графику [k = f(m, l)] в соответствии с требованиями ГОСТ 8.207. Примечание — Погрешность, возникающая при использовании формулы (5) для суммирования НСП и при нахождении поправочного коэффициента k для доверительной вероятности Р = 0,99 по графику [(k = f(m, l)], не превышает 5 %.

Главное для нас это то, что фактически вычисляется среднеквадратическое значение аргументов, в качестве которых принимаются конкретные границы индивидуальных погрешностей, задаваемых в привычной нам форме типа ±Х (дБ или В – не существенно).

И последняя существенная цитата:

7 Оценивание случайной погрешности и стандартной неопределенности, оцениваемой по типу А, результата измерения 7.1 Доверительные границы случайной погрешности и стандартную неопределенность, оцениваемую по типу А, результата измерения вычисляют следующим образом. 7.1.1 Если случайные погрешности представлены несколькими СКО Si, то СКО результата однократного измерения вычисляют по формуле . (9) Учитывая условия 7.1.1, стандартную неопределенность, оцениваемую по типу А, результата однократного измерения uА вычисляют по формуле , (10) где т — число составляющих случайных погрешностей; ui, A = Si. Доверительную границу случайной погрешности результата измерения e(Р) вычисляют по формуле , (11) где ZP/2 — Р/2 точка нормированной функции Лапласа, отвечающая вероятности Р. При доверительной вероятности Р = 0,95 Z0,95/2 принимают равным 2, при Р = 0,99 Z0,99/2 = 2,6. 7.1.2 Если случайные погрешности представлены доверительными границами ei (Р), соответствующими одной и той же вероятности, доверительную границу случайной погрешности результата однократного измерения вычисляют по формуле: (12) 7.1.3 Если случайные погрешности представлены доверительными границами, соответствующими разным вероятностям, сначала определяют СКО результата измерения по формуле , (13) а затем вычисляют доверительные границы случайной погрешности результата измерения по формуле (11).

Всё вышеприведённое вполне реализуемо, «освящено» многими десятилетиями практического применения, без малейших проблем пройдёт метрологическую сертификацию в органах что Ростеста, что Воентеста и позволит реально (хотя бы в этом, в расчёте погрешностей) соответствовать требованиям Федерального Закона №102 «Об единстве средств измерений» нашим многострадальным Методикам. Да и требованиям ГОСТ Р 8.563–2009 Государственная система обеспечения единства измерений. Методики (методы) измерений. Всем!

Разумеется, это лишь начало работы. Необходимо, всё же, покончить с оставшимся «в наследство» методом «закладки запасов». Мы не настолько богаты, чтобы бездумно тратить средства на защиту много больше, чем это нужно.

Сами методы измерений должны пройти внимательнейший метрологический анализ. На базе богатейшего опыта, заключённого в системе метрологических стандартов, не столь уж и сложно установить реальные (а не надуманные) границы погрешностей метода.

Подумать нужно и о погрешностях условий измерения. Во многих случаях их влияние, практически, сказываться просто не будет, так как ничего не меняется. Например, при стендовых (лабораторных) СИ (ПЭМИН, АЭП и т.д.) в течении одной рабочей смены и без отключения средств измерения. А вот при СИ АВАК двух ВП, размещённых на втором и 12 этажах здания изменение высоты однозначно скажется на результатах. Точно так же, как изменение температуры воздуха с утра (скажем, +17^o С) и в 16 часов (+34^o С). Насколько? Вот и нужно выяснять. Примеров можно привести множество и все они должны быть оценены, какие-то отброшены, как несущественные. Для каких-то установлены обоснованные границы погрешности.

Это нормальная инженерная работа. А дальше, дальше всё есть готовое. Ничего придумывать не нужно, только воспользоваться тем, что давно существует.

И тогда от «гадания на кофейной гуще» и «шаманства с антенной» мы все, наконец, начнём измерять. Как и положено специалистам…

В заключение хочется напомнить, что не столь давно действовало «оригинальное» предложение (формально присутствующее в одной из Методик до сих пор!) ничтоже сумняшися ВСЕ положительные значения погрешностей для «сигналов» брать со знаком «+», а все отрицательные, со знаком «-» для «помех». Понадобилось больше трёх лет и множество весьма авторитетных заявлений, чтобы дезавуировать этот образчик «имперской физики» на самом высоком уровне. Не дай нам бог повторения…