Испытательная лаборатория. К вопросу оценки САЗ.

Автор: Кондратьев А.В.

Поговорим теперь, отвлёкшись на некоторое время от, собственно, устройств ПЭВМ, об оценке активных средств защиты. То есть о том, что в принятой терминологии именуется аббревиатурой САЗ (системы или средства активной защиты). Разумеется, в применении к защите от утечки по техническому каналу за счёт ПЭМИН.

Как и следует из формулировки канала утечки, задача разбивается на две подзадачи, на защиту (а, следовательно, и на оценку эффективности) в свободном пространстве и в отходящих (или близко проходящих) линиях.

Начнём, привычно, с первого.

Итак, с точки зрения физики и теории радиотехники, задача защиты формулируется как обеспечение некоторого, заданного нормативными документами, отношения сигнал/шум. И не «где-нибудь», а везде, где может оказаться «супостат со средством перехвата». Причём под «сигналом» подразумевают пиковое значение энергии сигнала, а под «шумом» - среднеквадратичное значение помехового сигнала от САЗ. Всё это измеряется и вычисляется в некоторой, отдельно задаваемой, полосе частот.

В предыдущих публикациях многократно упоминалось о суммировании сигналов в полосе 1/τ. Именно в этой полосе, чаще всего, и рассчитывается требуемое отношение сигнал/помеха. Собственно, ничего хоть сколько-нибудь необычного в вычислении энергии сигнала нет.

Либо нам удалось с помощью тест-режима заставить работать интересующие нас цепи, линии, узлы, блоки технического средства с постоянной тактовой частотой кодовых посылок. И тогда спектр ПЭМИН «с точки зрения» узкополосного приёмного устройства имеет линейчатый характер. Либо не удалось по причинам, изложенным ранее. И тогда спектр будет носить характер сплошного (обычно некими зонами, полосами частот).

В обоих случаях можно и нужно рассчитать энергию, «умещающуюся» в заданной полосе, что и иллюстрирует рисунок 24.1.

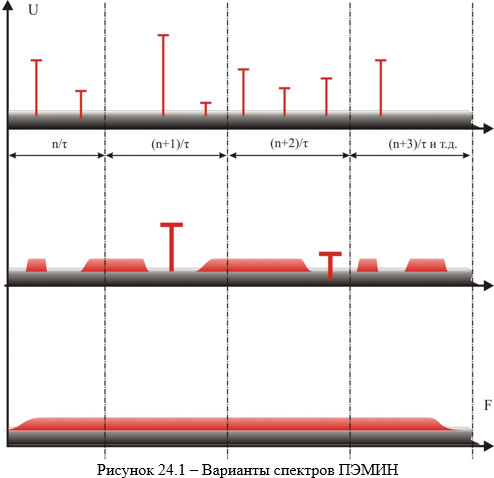
На верхнем спектре представлен «линейчатый» вариант, на нижнем – «сплошной», а на среднем – некий промежуточный и достаточно часто встречающийся вариант.

Не приводя тут конкретной расчётной формулы (специалистам она, несомненно, знакома), отметим лишь, что в числителе выражения (приведённого исключительно для «линейчатого» варианта спектра) суммируются энергии отдельных, измеренных в оговоренных условиях, частотных составляющих спектра ПЭМИН. Причём суммируются не сами измеренные величины (в мкВ/м), а их квадраты, что пропорционально энергии. Несложно вспомнить формулы, связывающие напряжение, ток и мощность. Кроме того, выполняется нормировка по полосе частот. Деление на тактовую частоту каждой частотной составляющей переводит расчётную величину в спектральную плотность энергии (мощности) на единицу ширины полосы (на 1 кГц), а последующее умножение полученной спектральной плотности на 1/τ «собирает» мощность во всей полосе суммирования. То есть в результате математических действий мы получаем гипотетическую мощность сигнала в полосе суммирования.

Итак, осталось понять, что же делать со сплошным или «линейчато-сплошным» спектром «опасного сигнала». Ну, с «линейчатыми» его составляющими – понятно. А с участками сплошного спектра? Опять же, НМД не предусматривает, но физика существует независимо от людских ошибок ;) Посему поступаем точно так же, как и неоднократно описывалось ранее. Кстати, взглянув на расчётное выражение в методике мы узрим, что не так уж и «новаторски» мы поступим, поскольку с сигналом от САЗ, имеющим принципиально сплошной (причём – неравномерный по частоте) спектр поступают именно «по физике», то есть рассчитывается интеграл всё в той же полосе 1/τ. То бишь всё то же суммирование квадратов измерений полосою приёмника. При этом полосы пропускания «прижаты» друг к другу, то есть шаг перестройки приёмника равен ширине полосы пропускания. Ну уж коли «закон» в виде НМД предписывает такую операцию для сигнала САЗ, то она столь же законна и для широкополосного сигнала ПЭМИН.

Таким образом, для сплошного или участков сплошного спектра поступаем как с сигналом САЗ, а с «линейчатыми» составляющими – как обычно. Затем общая сумма квадратов, как обычно, делится на тактовую частоту и домножается на 1/τ. Всего-то и делов ;). Даже «модификация» расчётных выражений НМД, практически, не нужна, использовано только то, что в них и так есть.

О том, как обработать сигнал САЗ (измерить и рассчитать), как любой широкополосный, в более ранних публикациях всё написано, повторяться нет смысла.

Вот о чём стоит поговорить, так это о том, как измерять. Если об измерениях «опасных сигналов» уже достаточно много сказано (в том числе – в НМД), то тонкостей измерений САЗ мы, пока, не касались.

В НМД нет главного, совершенно необходимого, для единообразного, физически корректного измерения..

Обращу внимание читателя на то, что для «опасного сигнала» предписано измерять максимумы. И по размещению измерительной антенны и по её ориентации в пространстве (ориентации диполей и/или рамки). Запомним – МАКСИМУМ! А сами «опасные сигналы» - просто все (в первом приближении).

А вот в отношении измерения сигнала САЗ – точно как у Шекспира: «Дальнейшее – молчание…».

Точнее – одно «указание» есть – измерять в направлении от «объекта» к «хххххххх ххххххх ххххх» (не надейтесь, цитаты не будет :-Р). О физической и функциональной корректности данной формулировки можно спорить, но… как писал Чехов: «Если Вам подали кофе – не старайтесь искать в нём пиво!» (самое главное «не старайтесь…!»)

Но вот об ориентации антенны в НМД ничего, ни словечка… Давайте думать!

По логике и физике возможно было бы поступать двояко:

• Ориентировать антенну по минимуму сигнала САЗ;
• Ориентировать антенну так, как она была сориентирована при измерениях «опасного сигнала».

Оба подхода имеют свои «плюсы» и «минусы». Но попытки описать их всё время приводят меня к необходимости рассмотрения постулатов и утверждений, непригодных для обсуждения в открытой среде. Поэтому я лишь называю проблему, а решать её придётся Вам самим и представителям Вашего регулятора (у кого есть сильное желание – приезжайте к нам на курсы!). А решать надо обязательно, разброс результатов измерений уровней сигналов САЗ от ориентации антенны легко достигает десятка – другого дБ. «Цена» вопроса», Вам, надеюсь понятна.

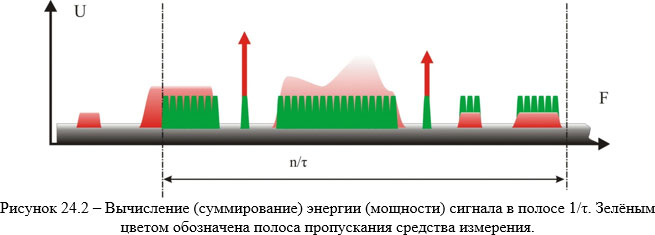
Есть ещё одно соображение. Как видно из рисунка 24.2 измерение участков сплошного спектра сигнала рекомендуется выполнять так же, как и сигнал от САЗ – «сплошняком», с шагом, равным полосе пропускания приёмника. В автоматическом режиме на это, сегодня, способна только система «Сигурд», причём версии ПО не ниже 5.0. (система «Сигурд» проходит полосу частот более 1 ГГц менее, чем за 7 минут). Всё остальное – ручками… Когда это 5÷10÷25 МГц – нудновато, но исполнимо. Но для сигналов САЗ это сотни МГц, что для ручного режима превращается в проблему и немалую (по затрачиваемому времени и усилиям). Как указывалось раньше, если огибающая спектра плоская, то всё сильно упрощается. Ну а если нет? Как именно распределить точки измерения по частотам полосы 1/τ , если их задать меньше, чем «сплошной» замер?

В НМД есть некие намёки на указания на сей счёт, но не более. Рискнём заглянуть за горизонт и рекомендовать для особо ответственных случаев распределять точки измерения так, чтобы результаты замеров сигналов в них (в любых двух смежных) отличались не более, чем на 3 дБ. Для менее ответственных случаев – на 6 дБ. Количество точек у Вас снизится в 10÷100 раз, что нельзя не приветствовать. Сигнал (неважно, САЗ или ОС) в промежуточных точках легко восстанавливается обычной линейной интерполяцией (прямо по значениям в дБ). Возникающая при этом погрешность много меньше, чем погрешность наших измерений. При таком подходе даже вручную работа оказывается вполне выполнимой. Кстати, приведённый метод, по сути, есть рекомендованный метод приблизительного численного интегрирования методом «прямоугольников», так что и с методической стороны тут всё «чисто». Только не надо путать, где надо оперировать абсолютными значениями в размерности напряжённости поля, а где можно работать с относительными величинами в дБ.

Исходя из вышеизложенного, просто считаем, что сигнал САЗ мы тоже измерили. Как и реальное затухание (если это требуется по условиям объекта), раздельно, для ПЭМИН и для сигнала САЗ.

Коли так, то осталось только всё подставить в расчётное выражение и рассчитать отношения сигнал/шум для всех полос суммирования, которые надо оценить, причём, уже на границе КЗ.

Есть ещё пара – другая утверждений, которые нигде не написаны «пером», но, несмотря на это, ни «вырубать» их начисто, ни принимать на веру без оговорок я не советовал бы.

Первым из них я бы назвал утверждение, что если мы измерили отношение сигнал/помеха в некой точке пространства (обычно вблизи защищаемого ТС), то в любой другой точке, на бóльшем удалении, это отношение останется таким же. Утверждение верное, но не при любых исходных условиях. Давайте рассмотрим графики ослабления («закона затухания») сигнала с увеличением радиуса. Для классического случая, то есть хрестоматийного распространения волны над проводящей поверхностью в свободном пространстве. Если мы начнём учитывать влияния строительных конструкций, стен, проводящих линий, то на анализ нам понадобится эдак с месячишко, неплохо бы иметь под руками пару «Эльбрус»-ов и т.д…..

Итак, три варианта взаимного размещения источника ОС («опасного сигнала») и сигнала САЗ (варианты понятны из рисунка 24.2). Вспомним, что электромагнитная теория не слишком строго описывая поведение поля в ближней и промежуточной зонах, тем не менее, утверждает:

• в ближней зоне поле спадает, приблизительно, обратно пропорционально кубу радиуса (~1/r³);
• в промежуточной зоне поле спадает, приблизительно, обратно пропорционально квадрату радиуса (~1/r²);
• в дальней зоне поле спадает обратно пропорционально радиусу (~1/r).

Не претендуя на точное соответствие масштабов, тем не менее, построим варианты размещения и спадания поля. Сразу обращу внимание читателя на то, что не указываю частотные границы между «ближней», «промежуточной» и «дальней» зонами. Специалисты прекрасно знают, как именно это сделано в руководящих документах.

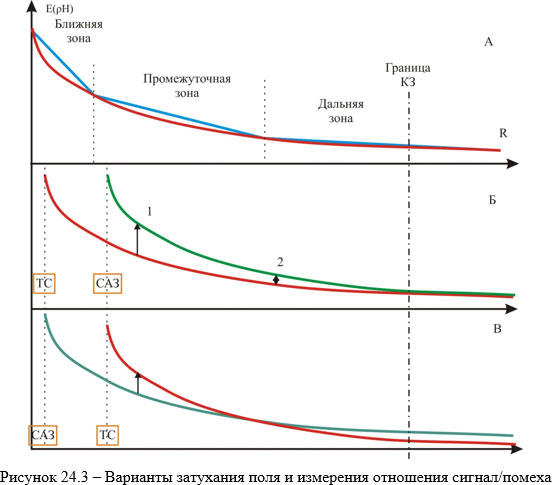
На графике «А» приведён условный закон затухания поля. Красная линия – реальное затухание, зелёная – его кусочно-линейная аппроксимация, применяемая на практике.

На графиках «Б» и «В» приведены два варианта, в которых ТС и САЗ (излучающая антенна САЗ) размещены на разных удалениях от границы КЗ. Как хорошо видно, в варианте, когда САЗ ближе к границе КЗ отношение сигнал/помеха от точки 1 к точке 2 уменьшается. То есть снижается защищённость. Кажущийся парадокс, но всё (хоть и не в масштабе) строго «по физике». А вот в варианте «В» с расстоянием (от точки 1 к точке 2) отношение сигнал/помеха только увеличивается, что «есть добро» J. Вариант с нахождением ТС и САЗ в «одной точке» не рассматривается в связи с его очевидностью. Выводы, коллеги, сделайте сами.

Второе утверждение, которое стоило бы рассмотреть, тоже относится к затуханиям сигнала и помехи, но в линиях, а не в пространстве и будет рассмотрено ниже.

Есть ещё одна особенность, которую, порою, необходимо учитывать. Всё приведённое выше в части типового затухания поля (имеются ввиду пресловутые зоны ~1/r3; ~1/r2; ~1/r1) относится только к случаю, когда излучатель (неважно, «случайный» или некая антенна) является «точечным», то есть весьма малым по сравнению с расстоянием от него до точки размещения измерительной антенны. Если Вы, например, возьметесь экспериментально проверять закон затухания с расстоянием магнитной компоненты поля на частоте 1 МГц от рамочной антенны со сторонами 5·20 м, то на первых 50 м я не возьмусь даже предсказать, какой «закон» затухания у Вас получится. Показатель степени у «r» легко может оказаться и 5, и 17/4 и т.д., причём он будет изменяться с расстоянием Это – только экспериментально. Тем более, что на реальном объекте погрешности, вносимые каркасом здания, токопроводящими коммуникациями и т.д. огромны и непредсказуемы.

На этой «мажорной» ноте позволю себе закончить с приключениями волны в пространстве и взглянуть на то, как она поведёт себя в токопроводящих коммуникациях (пользуясь терминологией, принятой в проблематике – в «линиях»)

Вначале чуток теории, которая большинством из нас сдавалась давно и …лучше промолчать и перейти к сути J

Вот и позволю себе начать с опровержения своих же (и не только моих!) слов. Цитирую: «как она поведёт себя в токопроводящих коммуникациях…». Так вот, никак себя электромагнитная волна в токопроводящих коммуникациях не ведёт. Вообще и никогда. Поскольку электромагнитное поле в проводящей среде существовать не может в принципе! Ну как, спрашивается, можно себе представить электрический вектор в проводнике???? А никак, не существует он в проводящей среде. Вспомним «скин-эффект», в любом проводнике электромагнитное поле вытесняется за пределы проводника. То, что называется «глубиною проникновения» на радиочастотах для проводника типа меди составляет сотые и тысячные мм.

Посему, уж если говорить о поле, то распространяется оно ВДОЛЬ проводника, в области пространства, к этому проводнику примыкающей. Проводник, как справедливо напоминает нам товарищ В. В. Никольский, который и по сей день остаётся одним из лучших авторов учебников по электродинамике и распространению радиоволн, является направляющей системой, не более, но и не менее. Написанное легко качественно иллюстрируется графиками напряжённости поля в проводнике и ближайшей к нему области пространства (рис 24.4).

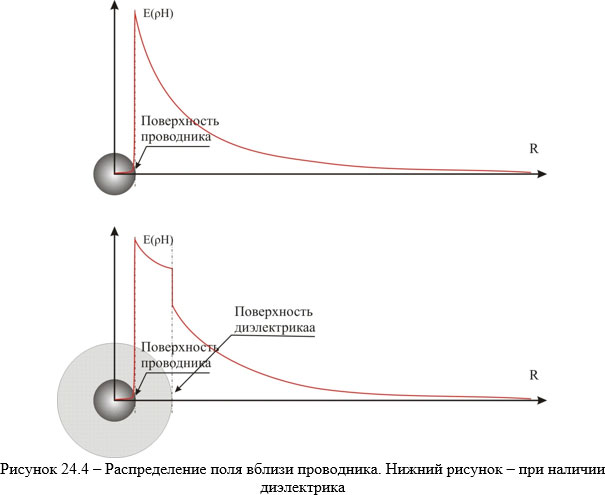
Как видно из рисунка, поле концентрируется либо в изоляторе проводника, либо (при его отсутствии), в ближайшей к проводнику зоне пространства. Строгое, количественное доказательство качественной картины заняло бы немало места и сложных выкладок. А вот аналогия простейшая проста, особенно для случая проводника в изоляторе. Это распространение света в пространстве между двумя коаксиальными зеркальными цилиндрами. При этом внутренний цилиндр-зеркало металлический, а внешний – диэлектрический. Разумеется, это картина только качественная и верная для случая, когда проводник весьма удалён от любых других проводников. В практике термин «весьма» означает, что это удаление много больше длинны волны. Посему, практически не бывает J

Электродинамику мы вспомнили (сие лишним никогда не бывает!), двинемся дальше. Поскольку рассмотрение вопроса посвящено оценке эффективности САЗ, то, собственно, надо рассматривать наводки на линию (будем продолжать называть «привычно неправильно») от двух независимых источников – источника «опасного сигнала» и антенны САЗ.

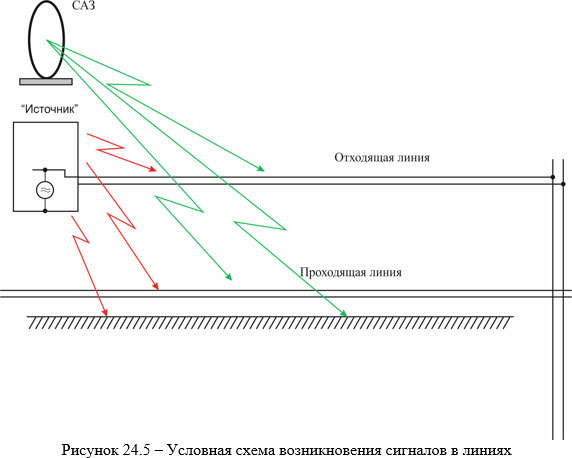
Из приведённой схемы следует, что наводка через ПЭМИН, точнее – её условия, в первом приближении, почти (за исключением просачивания ОС в отходящую линию непосредственно в самом ТС) одинакова для всех транспортирующих (направляющих) систем, которые подлежат рассмотрению. Да, расстояния от источника излучения, в общем случае – разные, что тоже должно учитываться в последующих рассуждениях. Но эти отличия, как правило, ограничиваются первыми десятками см – первыми единицами м.

Что означают с точки зрения электродинамики разность этих расстояний? Ну, прежде всего – разность энергетики. То есть на каждый, более удалённый по радиусу от ТС участок линии (любой, включая заземлённую арматуру в перекрытии пола) падает волна с меньшей энергией.

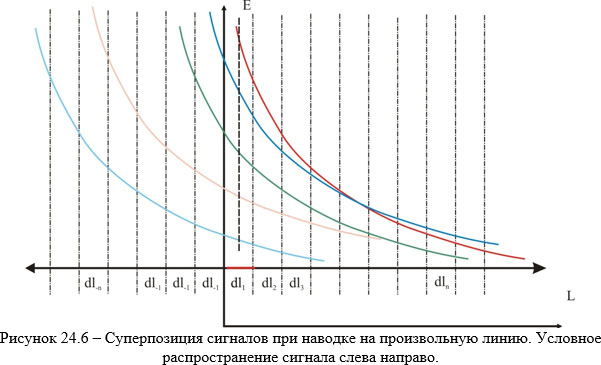
Как нетрудно видеть, к рассматриваемому участку dl₁ сигналы приходят от других участков с разными амплитудами (не надо забывать и о том, что на рисунке не показано. Существует и распространение сигнала в обратном направлении, от участков dln влево. Кроме того, на рисунке иллюстрировано сложение модулей, поскольку различные фазы на плоском рисунке показать невозможно. В первом приближении надо помнить, что групповая скорость распространения волны в транспортирующей системе всегда меньше, чем в свободном пространстве. Поэтому фаза волны вдоль проводника всегда отстаёт от фазы падающей из пространства волны. Из рисунка следует, что всё более удалённые по длине линии элементарные участки dl_n влияют на рассматриваемый dl₁ тем меньше, чем дальше они расположены. Степень этого спадания зависит, в первую очередь, от погонного затухания ВЧ-сигнала в транспортирующей системе. В технике проводной связи существует понятие «электрической длины линии», как раз и определяющееся этим фактором. Обычно, с достаточной степенью приближения, она принимается равной (7÷10)λ.

Сам процесс наводки тоже не слишком прост. В каждой точке линии (бесконечно малом участке линии dl) вектор поля (для простоты будем рассматривать, например, электрическую компоненту), распространяющаяся волна будет результатом суперпозиции (сложения, векторного, естественно) бесконечного (в общем случае) сигналов, наведённых на другие участки dl и поля, падающего именно на этот участок из пространства. Это иллюстрировано рисунком 24.6

Причём всё вышеизложенное качественно верно, если в рассматриваемой линии установился режим «бегущей волны». То есть линия, как минимум, для рассматриваемого диапазона частот, согласована. То есть, нагружена на своих концах на нагрузки, равные её волновому сопротивлению и не имеет заметных неоднородностей.

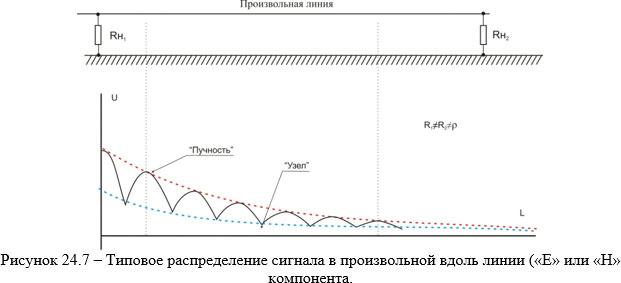
Вот это-то, последнее, условие на практике, для произвольных линий (электропитания, сигнализации, телефонии и т.д.) не выполняется никогда! Вдоль линии всегда устанавливается смешанный режим с КСВ (коэффициентом стоячей волны от 2 до 10). Обычная «картина» сигнала ВЧ в произвольной линии легко выявляется при помощи обычного токоизмерителя и иллюстрировано рисунком 24.7. Автору даже на специально сконструированной линии, размещённой строго на одном расстоянии над заземлённой поверхностью, физически почти однородной, ни разу не удалось получить КСВ лучше 2,5÷3. Сильно похоже, что для не специфицированных линий это невозможно вообще. Не верите на слово – проверьте сами, это не так сложно. Сразу предупрежу, что не все мои коллеги согласны с тем, что за такое распределение сигнала в линии, как показанное на рис. 24.7, отвечает именно несогласованность и неоднородности в линии. Но, поскольку я экспериментировал, и со степенью рассогласованности «на концах», и с созданием неоднородностей, другого корректного объяснения предложить не могу. А что в любой линии на любой (естественно, за исключением самых низких, на которых длина волны больше участка линии) частоте выявляется именно такой характер распределения – ручаюсь. Кстати, стоит упомянуть, что «шаг узлов» (они выявляются более чётко, чем «пучности») как раз совпадает с длиною волны, с учётом диэлектрической проницаемости диэлектрика линии. Для большинства практически применяемых диэлектриков (полихлорвинил, полиэтилен, полистирол) значение ε≈ 2÷2,5. Как раз «в корень» из этой величины уменьшается длина волны вдоль линии, всё по теории.

По нашим исследованиям волновое сопротивление достаточно произвольной линии в интересующем нас диапазоне частот меняется (от низких частот к высоким) от сотен Ом до первого десятка Ом, то есть весьма значительно (модуль «ρ», естественно). Соответственно согласовать линию даже специально весьма проблематично. А уж реальная линия…

Почему измерять не пробником?

А вот об этом сейчас и поговорим.

Ещё раз взглянем на рисунок 24.5. Если говорить о некой, для простоты двухпроводной линии, нетрудно видеть, что оба её проводника, размещённые весьма близко друг к другу, находятся под, практически одинаковым воздействием падающей волны. Естественно, что в этих условиях на оба проводника наведётся один и тот же, как по амплитуде, так и по фазе, сигнал. То есть эти два проводника, практически, эквипотенциальны. Соответственно, некий двухполюсный пробник, подключённый к этим двум проводникам, ничего, кроме тождественного «нуля» показать не способен.

Далее будем рассматривать эту линию по отношению к некой «земле», тем не менее тоже (неизбежно!!!) находящейся под воздействием той же пространственной волны. Картина качественно меняется. Амплитуда и, главное – фазы, воздействующей волны становиться разными. Насколько? «А кто ж там разберёт?». Непредсказуемо, в общем и целом. Соответственно столь же непредсказуемыми становятся и результаты такого «измерения». Зато токоизмеритель, принципиально «не обращая внимания» ни на что, через его отверстие не проходящее, точно нам выдаёт напряжение, пропорциональное протекающему через него току. Что, собственно, и требуется.

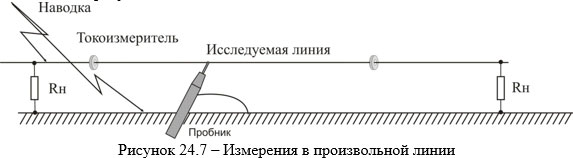
Разумеется, «смешанный режим» в линии никуда не денется. И токоизмеритель будет бесстрастно фиксировать максимумы и минимумы сигнала вдоль линии. Но их общая тенденция, степень затухания вдоль линии (красный или зелёный пунктиры на рисунке 24.6) измеряются без проблем. Пробником же измеряется полная ахинея, особенно если учесть тут же наводку на корпус средства измерения, находящегося поблизости. Наводку на экран кабеля от пробника до средства измерения и т.д. Я уже не говорю о том, что подключение пробника просто невозможно в любой требуемой точке. Никто не позволить сдирать изоляцию с кабеля по прихоти «сишника». А замер в одной – двух точках вообще ни о чём не говорит.

Ну вот, «лирико-электродинамическое» отступление было, по необходимости, довольно длинное и пора вернуться к измерениям САЗ.

Собственно, осталось немногое. Сразу надо оговориться, что если «опасные сигналы» частенько (хотя, как мы видели ранее – не всегда) сосредоточены на вполне определённых частотах, то сигналы САЗ принципиально широкополосны, даже сверхширокополосны. Когда имеем дело с такими сигналами, то описанная выше картина «стоячих волн» немедленно исчезает. Несложно себе представить, что бесконечная сумма разных частот даст и бесконечную сумму стоячих волн, максимумы и минимумы которых придутся на разные участки линии. В результате – благостная картина «псевдобегущей волны». Тем не менее, измерять чисто практически проще токоизмерителем и уж точно безопаснее, особенно на линиях электропитания. Остаётся последний вопрос. Токоизмеритель измеряет ток вблизи линии (как и следует из названия). А по ряду причин нам бы нужно было иногда знать и напряжение…

Если результатом должно быть отношение сигнал/помеха, то «по току» или «по напряжению» совершенно безразлично, численно эти два отношения будут равны. Но если нам понадобилось именно напряжение (строго говоря, модуль «Е» вектора волны вблизи линии), то без знания волнового сопротивления линии не обойтись. По сути всё тривиально, по закону Ома, Е=I*R. Откуда же взять это самое R?

Можно измерить, значение частотнозависимо, посему на многих частотах и аппаратура для таких измерений не самая простая, как и процедура измерений на ВЧ частотах. Есть рекомендация проще. Поскольку мы всё равно уже, как только заговорили о применении токоизмерителя, вышли из «зоны» действия НМД (где тупо указано измерять пробником!), то надо идти до логического конца J

Проблема измерений ВЧ в произвольных линиях стара как и сама радиотехника. И выдумывать ничего особенного не надо… В проблематике вопросов электромагнитной совместимости, весьма близкой «по идеологии», давным-давно столкнулись с тем же самым. В частности – при применении для близких измерений «эквивалентов сети», включаемых «в разрыв» исследуемой линии. Чтобы эти эквиваленты не вносили слишком заметную неоднородность, их сопротивление должно, в какой-то мере, повторять волновое сопротивление линии. Вот и заглянем, например, в ГОСТ Р 51319-99 «Совместимость технических средств электромагнитная. Приборы для измерения индустриальных радиопомех. Технические требования и методы испытаний», в раздел 4.3 «Требования к эквивалентам сети» (Указанный ГОСТ есть в электронной библиотеке ДО). Там приведены и аналитически и графически модули полного сопротивления эквивалентов сети для различных частот. А в самом грубом приближении на частотах самых низких, до 100-150 кГц можно принимать сопротивление произвольной линии равным 150 ом, до 30 МГц – 75 ом, выше – порядка 50 ом (в наших экспериментах спадало до 20-30 Ом). К слову – наша лаборатория СИ именно так и поступает. Пока «рекламаций» на то, что мы выходим за пределы действующей методики, не поступало.

И последнее, о САЗ по отношению к линиям. Все расчёты, естественно, выполняются так же, как и для «эфира», если по условиям объекта ОС и сигнал САЗ поступают в разные участки линии, то необходимо измерение реального затухания раздельно, для этих сигналов. «Фокусы» тут бывают разные и вполне могут проявиться эффекты, похожие на те, что иллюстрированы рисунком 24.3. «Механизм» погонного затухания в транспортирующей системе (вблизи линии) более сложен, чем в пространстве. А в конкретной, проложенной на объекте, порою с многочисленными переходами из кабеля в кабель, ответвлениями и т.д. (неравномерности!!!) затухание вообще непредсказуемо. Но в общем и целом об измерениях реального затухания надо говорить отдельно.

Надеюсь, что изложенное поможет коллегам с бóльшей ясностью и ответственностью подходить к оценкам эффективности САЗ.